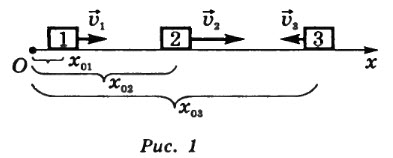
Зависимость кинематических величин от времени можно изобразить графически. Изобразим графики скорости, перемещения, пути и координаты для трех тел: 1, 2, 3 (рис. 1).
Тела 1, 2 движутся в положительном направлении оси \(Ox\), причем \(v_2\)>\(v_1\). Тело 3 движется в направлении, противоположном оси \(Ox\); их начальные координаты соответственно \(x_{01}\), \(x_{02}\), \(x_{03}\).
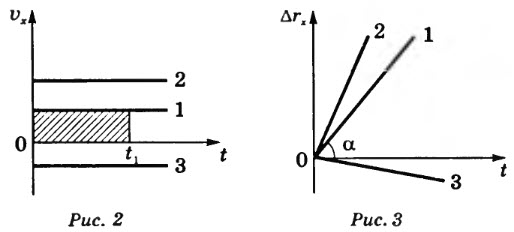
Графики скорости представлены на рисунке 2. Площадь заштрихованного прямоугольника численно равна пути \(S\) (модулю перемещения), пройденному телом 1 за время \(t_1\). На рисунке 3 даны графики перемещения, на рисунке 4 — графики пути.
Наклон графика пути к оси времени зависит от модуля скорости:
\[\operatorname{tg} \alpha = v_x\]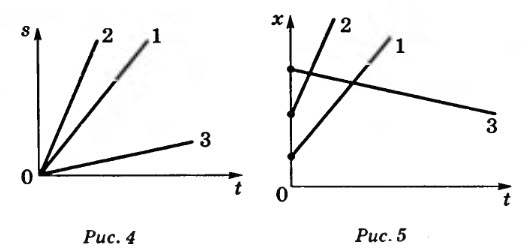
Графики движения (зависимости координаты от времени) изображены на рисунке 5.
С помощью графика движения можно определить:
- координаты тела в любой момент времени;
- путь, пройденный телом за некоторый промежуток времени;
- время, за которое пройден какой-то путь;
- кратчайшее расстояние между телами в любой момент времени;
- момент и место встречи тел
- и др.


